行動の決定論的規則は完全に予測可能な事象を生じる。本当だろうか？

カオスには２種類の意味があるから気をつけておくれ。一つは哲学としての「全くの混沌」だ。複雑系では「カオス」は、ひどく予測不可能だけど基本的には決定論として使われる。

カオスは１９６１年ローレンツという気象学者が発見した数学モデルであった。

彼が、天気予報を正確に予測しようとして、コンピューターで３回予測したろこと、３回ともまったく違う答えがでたところから疑問は始まった。

追求の結果、最初の予測は少数点以下が６桁でであるのに検算は小数点以下を３桁で計算していたことが原因であることが分かった。

従来数学では小数点の違いは、予測の精度の違いぐらいにしか影響を及ぼさないと考えられていたが、最初のわずかな違いは全く違う結論を導き出す。これを初期値敏感性という。

この現象を３つの連立方程式にまとめたのが、最初のカオスモデルである。

初期値がちょっと変わっただけでとんでもない結果がでてくる例をあげよう。

例えばＤ＝C/（A-B）を計算してみよう。A=100,B=99,C=100ならD=100となる。

ではAの値を1%だけずらして101としてみる。するとD=50に半減してしまう。

もしもAを９９にしてみよう。もう言わないほうがいいくらい恐ろしい結果になる。

その後１０年の後、ウィーナーによってカオスと命名された。

初期条件を与えれば、未来予測が可能とするニュートン力学を大きく覆し決定論の対局にこのカオスは位置するものとなった。

数学的には決定論にしたがう。しかし、観測や数式によるあらゆる未来予測、構成予測は観測機械の精度や、小数点何桁まで数学モデルに組み込むかで、近似値ではなく全く違う結果が出されるのでは、根源探しも同時に意味をなさなくなった。

これは自然界における普遍的な現象という認識とされる。

ローレンツアトラクター 1963年

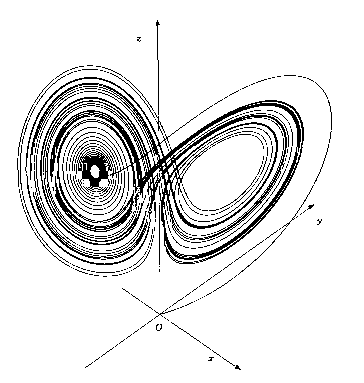
一般語では「メチャクチャ」にとらえられることがあるが、これは間違えである。科学においてはカオスとは基本的には決定論であり、ただ、初期値敏感性が全体に複雑に無限に影響を与えるという意味であることを再認識してもらいたい。ただその計算が複雑なだけなのだ。

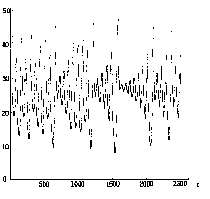
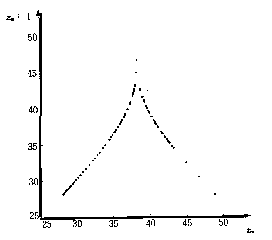
インターネットはカオスのネットといえる。それ故の難しさとそれ故に魅了されるものがあるなだ。つまりカオスは人を魅了するものがあるということになる。

いままで小川の渦やひらひら落ちる雪の動きなんて、「ただ自然であるだけ」と思われていた。でもそこに科学のメスを入れてみたら普遍的な領域があることに気がつき始めたんだ

つまり、カオスは科学の新しい領域を切り開きつつあるといえる。いままでの科学はものごとを単純に単純にしてきたけど、この新しい科学の姿勢は複雑にどこまでも複雑に関連する領域を広げていく。その有効な道具はやっぱりコンピューターだね。

コンピューターは３つの側面で複雑系に貢献している。

一つは、シミュレーションだ。これによって今まで計測不可能だったことが次々に解明されてきている。

もう一つはカオスの実体を生成している点だ。インターネットを代表とするネットワークはカオスそのものだ。

北京の蝶が羽ばたいただけでニューヨークの天気がかわってしまうような世界をどうおもう？

人間の知恵の限界を悲観的にとらえることもできる。でも逆に主観的には自由な世界に生きていられるというとこにもなる。

それから蝶が世界の天気に影響をあたえているなら、僕や君たちの行動も世界や地球環境に影響をあたえて続けているっている自信のプレゼンスと何らかの役割を果たしているということ感じることができる。

ただし、非線形のすべてがカオスではない

ミクロがマクロにつながっていることを予測できる道具としてコンピューター

コンピューターは２０世紀最大の思想家ね

カオスの問題は化学の分野ではプリゴジンが研究している。

HOME

ご意見はparadigm@dreamドットコムまで