|
1975年 |
フラクタル (fractal) |
B・B・マンデルブロー |
万物のデザインの数学
自然界のデザインにはどこか共通したものがある。自己相似性という原理だ。これを数学的に表現しようというのがフラクタルだ。つまり同じ式の繰り返しから自然界のデザイン生成をしようというものだ。
この手法は、特に新しいものではない。こうした自己相似性により複雑な図式が生成されることは昔からコッホ曲線やシェルビンスキーのカーペットなどとして知られていた。それがコンピューター・シミュレーションの導入により急速に発達したというのが最近の動きだ。
→MIXIへhttp://mixi.jp/view_bbs.pl?id=116352721)まず線が一本あったとさ。
![]()
2)線の真ん中3分の1を三角におる
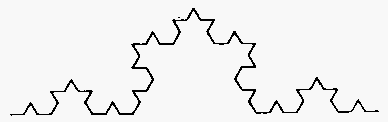

→MIXIへhttp://mixi.jp/view_bbs.pl?id=11635315
正方形を六分割して真ん中を切り取る作業を繰り返すと全体として次のような図形ができて、無限に入り込むことができる。まるで曼陀羅のようである。

フラクタル
こうしたことを原理とみたて体系化したのがフラクタルだ。
フラクタルによれば、無機物も複雑な生物のデザインも同じ自己相似性が見られるとしている。
上段の図形の全体構図をそれぞれに枝に置き換えてみる下段図形のようになっていく。
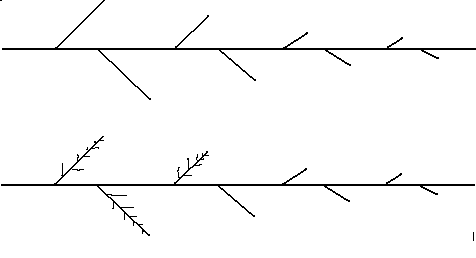
さらにその小枝に全体の構図を置き換えるといった具合に何回か繰り返すと、下図のような生物的デザインが完成する。

人類が最初に眼にしたフラクタル図形。発見者のマンデルブロー氏の名からきている。またフラクタルもマンデルブロー氏が付けたもの。
マンデルブローは「自然はフラクタル」であると言ったが、この意味は、自然の形成原理は「自己相似性」にあるという意味。つまり簡単な式を繰り返すと複雑さを形成することができる。それもちょっとした複雑さではなくって「無限の複雑さ」を形成できるということ。
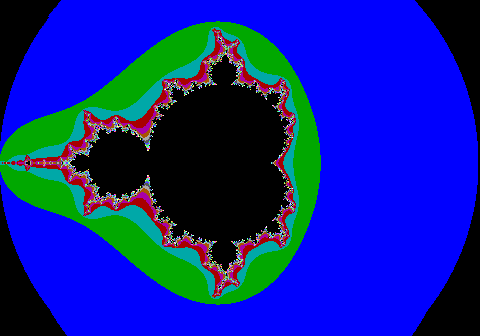
具体的には「Z→Z2乗+C」という簡単な式を循環させてあらわれる点を座標上に次々プロットしていくとこんな図になる。
こうした原理をもとにコンピューターでシミュレーションし、結果画面にあらわれたのは、マンデルブロー集合という終わることのない無限に込み入った複雑な模様だった。人によってはこれを神の原理を発見したという。
自己相似性にランダムをちょっと加えると、そこに現れるのは
カオスだ。フラクタルは自然界を見る目に革命を与えたのである。自然は、われわれが考えるほど滑らかでも連続的でもない
一度フラクタルの目を持つと自然界の至る所にフラクタル図形を見いだすことだできる。宇宙にもそれは見いだせる。土星の輪、天の川。建築家が家の設計を説明するように、複雑な雲の形を正確に相手に伝えられるかもしれない。
フラクタルによる宇宙構造の理論→
メガバースこのフラクタルは生命の起源説にも重大な影響をもたらしたようだ。生き物は簡単な法則の繰り返しからつくられているのではないか?
神経構造はフラクタル図で表されるし、肺はフラクタル構造によって表面積を広くしている。
DNAもその進化プロセスで同じ原理の繰り返しから生成されたという洞察がもたらされる。
これが原理であるとしたフラクタル理論によるAIのプログラムはDNAと同等な意味性を有することになる。
フラクタルは我々の感性にも潜んでいる。
自然の絵を書く書き手は筆で同じ動作を繰り返す。直感的にフラクタルをとらえていたのである。
ゴッホの絵を見てみるといい。同じ筆の繰り返しになっているだろ?
陶芸もフラクタル。釜から取り出した時に想いもよらない自然を発見することができるのである。
芸術性のなかにフラクタルが潜んでいるのはたしかだ。
では、なぜフラクタルは美しいのか?
フラクタルは秩序と無秩序の境目にある。そして我々もそこにいて、親和性が高いからだろう。
ネットワーク上でフラクタルの式だけを送信して相手画像を見せることもできる。
いくら拡大しても細部が再現可能な無限の解像度をもつ画像通信ができるわけだ。
しかしどんな図形にでも適用できる手法じゃない。フラクタル性を見つけやすいものに限られる。
生物の部分を取ってみるとすぐにフラクタルの構造があることに気がつく。この「部分」が「全体」を表すという考えを物質的にとらえずに時間でとらえるとまた違う世界が広がる。
構造としてのフラクタルもあるが時間のフラクタルもありえる。一時間の中に一生があるかもしれないし、人の一生と宇宙の一生が同じ式で運行されているかもしれない。
生命発展の歴史を母親はわずか10ヶ月で再現することができる。
これを母親から母親へと連綿と時間軸にならべてみると、まるでロシアの入れこ人形のようになる。
すなわち我々の一生は宇宙の一生の凝縮しているともいえる
はたしてこの原理は、個々の個体に対してのみ有効なのだろか?
DNAの起源に関与し、今の我々をも支配している原理は必ず、その間の何十億年のプロセスに影響を与えていると考えるはずがむしろ自然だろう。
巨視的な視野でみてみると進化のツリー図もフラクタルに見える。
進化の過程でフラクタル次元が違ってきている。
音楽のメロディー、リズム
バッハのブランデンブルクは炭素系の生物であれば気持ちいいだろうという理論のもとにボイジャーに詰め込まれてメッセージを乗せ宇宙に飛び出した。
f/1揺らぎ
扇風機:フラクタル強弱で風が吹くと思えば吹かずの心地よさを感じる。
心拍数:健康な人ほどf/1揺らぎがある。不健康な人ほど揺らぎがない
ひきこまれる話術なんかにもみられる
その疑問には、ちゃんと答えてあげないとね。
まず、要素還元的統一は、現状を尺度として、要素に還元すること。
フラクタルは「形態的統一」といえる。底がない、天井もない。基準になる尺度がない。つまり部分に分解してみてもそこにまたそれを構成する要素があらわれて、それを繰り返していくといつの間にか元に戻ったりしてしまう。
フラクタルは
カオスとよく似ている。似ているどころか一つの真理を違うが側からみているにすぎない。カオスの立場の人は自然を科学で「分析」するのに対して、フラクタルの立場の人は、自然を理論によって「合成」することに興味を持っている。フラクタル図の一点を時間変動でとらえるとカオスになる。
自己相似形の不安定性
フラクタルの研究そのものがフラクタル
学閥を越えて統合していく原理だ。
このシンポジウムのフラクタルの次元が高いものになることを望みます。
フラクタル次元とは, フラクタルの特性を表す数値であり, 物体の形状の複雑さを表す尺度としても用いられる. フラクタル次元が大きいほど, 対象形状は入り組んだものとなっており, この値は, われわれが慣れ親しんでいる2次元, 3次元といった整数値ではなく, 1.28次元とか2.75次元といった非整数値をもつものである. いま, 対象図形が相似比rのN個の部分(セグメント)から構成されているものと仮定する. このとき, 次の式を満たすDをフラクタル次元とよぶ.
rN1/D = 1 (4.4)
この式を用いて, 前出のコッホ曲線のフラクタル次元を求めてみると, 相似比が1/3の4個のセグメント(線分)から構成されているから, 式(4.4)より(1/3) × 41/D = 1, すなわち41/D = 3となる. 両辺の対数をとって, (1/D)log4 = log3から, フラクタル次元Dはlog4 / log3 = 1.26となる.
HOMEご意見はparadigm@dreamドットコムまで